The Open University - M248 TMA 03
The Open University Statistics - M248 TMA 03
Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.
You are advised to look at the general advice on answering TMAs provided on the M248 website.
Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions.
Note that the Minitab files that you require for TMA 03 are not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website.
Question 1, which covers topics in Unit 5, and Question 2, which covers topics in Unit 6, form M248 TMA 03. Question 1 is marked out of 28; Question 2 is marked out of 22.
You should be able to answer this question after working through Unit 5.
(a) In this part of the question, you should calculate the required probabilities without using Minitab, and show your working. (You may use Minitab to check your answers, if you wish.)
In England, the most serious emergency calls requesting an ambulance are classified as ‘Red 1’. According to data from NHS England, in March 2017, the London Ambulance Service (LAS) received a total of 1597 Red 1 emergency calls. Based on this number and adjusting for variations during the day, suppose that Red 1 calls arriving at LAS in daylight hours may be modelled as a Poisson process with rate 3 per hour.
(i) (1) Write down the distribution of the number of Red 1 calls arriving at the LAS in a 30-minute period during daylight hours, including the values of any parameters. [2]
(2) Calculate and report the probability that three Red 1 calls arrive at the LAS in 30 minutes during daylight hours. [2]
(ii) (1) Write down the distribution of the waiting time (in hours) between the arrival of two successive Red 1 calls at the LAS during daylight hours, including the values of any parameters. [2]
(2) Calculate and report the probability that the gap between the arrival of two successive Red 1 calls at the LAS during daylight hours will exceed 20 minutes. [4]
(b) This part of the question concerns data on the lengths of the 51 time intervals (in days) between successive earthquakes in California starting from a major earthquake on 9 January 1857, up to an earthquake on 24 August 2014. (To qualify for inclusion in this dataset, earthquakes had to be single mainshocks with magnitude of at least 4.9.) These time intervals are in the variable Interval in the worksheet california-earthquakes.mtw. In this part of the question, you will explore whether or not a Poisson process is a suitable model for these data.
(i) The intervals between successive events in a Poisson process are exponentially distributed. Using Minitab, find the mean and standard deviation of the intervals between earthquakes in California. Are these values consistent with the data being observations from an exponential distribution? Give a reason for your answer. [3]
(ii) Using Minitab, obtain a histogram with the following properties:
• the ticks on the horizontal axis are at the cutpoints
• the bins have width 500 days
• the first bin starts at 0 days and the last bin finishes at 7500 days. Include a copy of your histogram in your answer. Is the shape of the histogram consistent with the data being observations from an
exponential distribution? Give a reason for your answer. [4]
(iii) The data are listed in the order in which they arose. Using Minitab, produce an appropriate graph to investigate whether, for the period of observation, the data are consistent with the rate at which earthquakes occur in California remaining constant. Include a copy of your graph in your answer. On the basis of your graph, explain whether or not you think that the rate at which earthquakes occur in California remained constant over the course of the period studied. If you think that the rate did not remain constant, then say how you think it changed. [6]
(c) A certain form of ‘triangular’ distribution has c.d.f.
F(x) = 1 − (1 − x)2; 0 < x < 1;
which is plotted in Figure 1 below. (It is called a triangular distribution because its p.d.f. is a line which, together with the axes, forms a triangle.)
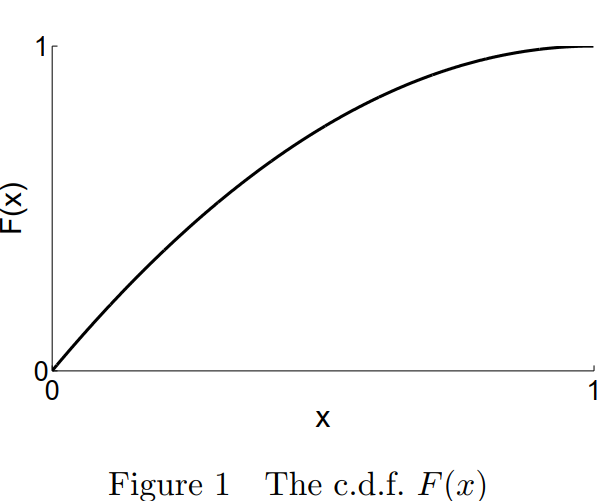
(i) Calculate the value of the upper quartile for this distribution. [3]
(ii) On a copy of, or very rough sketch based on, Figure 1, show the values of α and its corresponding quantile qα for the upper quartile that you calculated in part (c)(i). [2]
Question 2
You should be able to answer this question after working through Unit 6.
(a) In this part of the question, you should calculate the required probabilities using tables, and not Minitab, and show your working.
(You may use Minitab to check your answers, if you wish.)
A model for normal human body temperature, X, when measured orally in ◦F, is that it is normally distributed, X ∼ N(98:2; 0:5184).
(i) According to the model, what proportion of people have a normal body temperature of 99 ◦F or more? [3]
(ii) Find the normal body temperature such that, according to the model, only 10% of people have a lower normal body temperature. [2]
(iii) Let W denote normal human body temperature, when measured orally in ◦C. Given that W = 5 9(X − 32) and that
X ∼ N(98:2; 0:5184), what is the distribution of W ? [3]
(iv) According to the model you just derived for W , what proportion of people have a normal body temperature of between 36 ◦C and 36.8 ◦C? [4]
(b) The Minitab file body-temperature.mtw contains values of the normal body temperature, measured orally, of n = 130 people. The model for normal human body temperature used in part (a) of this
question was obtained partly by consideration of these data. The data can be used to check whether or not the assumption of normality of normal human body temperature is appropriate. Suggest a suitable graph to investigate specifically whether or not a normal distribution might be a good model for the normal body
temperature of people, measured orally. Using Minitab, produce this graph. Include a copy of your graph in your answer. On the basis of this graph, do you think that a normal distribution is a plausible model for
these data? Explain your answer. [5]
(c) Suppose that the mean weight of a particular type of ripe tomato is 155 g and the variance of the weight of this type of ripe tomato is 576 g2. A random sample of n = 36 such ripe tomatoes is obtained.
(i) What is the approximate distribution of the sample mean weight of the random sample of 36 ripe tomatoes? [2]
(ii) Use Minitab to find the probability that the sample mean weight of the sample of 36 ripe tomatoes lies between 150 g and 157.5 g. To show that you used Minitab, write down the results of any intermediate calculations you make in Minitab to the same number of decimal places as given by Minitab. [3]
Our statistics help experts have prepared the following sample solutions for you to compare.
M248 TM 03 open university statistics solutions for question 2.docx


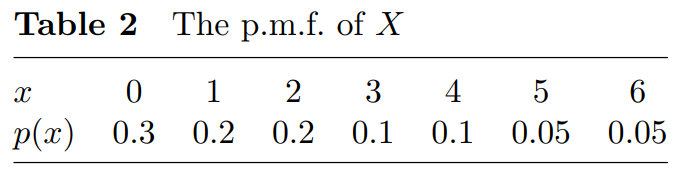
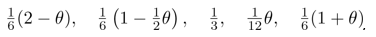
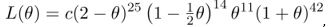 ,
,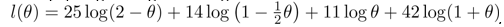 .
.