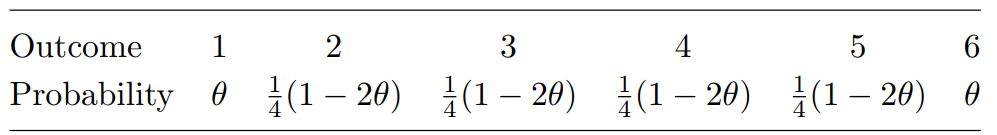Faculty of Science, Technology, Engineering and MathematicsM248 Analysing data

M248 - TMA 04

*Please read the Student guidance for preparing and submitting TMAs on the M248 website before beginning work on a TMA. You can submit a TMA either by post or electronically using the University’s online TMA/EMA
service.
You are advised to look at the general advice on answering TMAs provided on the M248 website. Each TMA is marked out of 50. The marks allocated to each part of each question are indicated in brackets in the margin. Your overall score for each TMA will be the sum of your marks for these questions. Note that one of the Minitab files that you require for TMA 04 is not part of the M248 data files and must be downloaded from the ‘Assessment’ area of the M248 website. For your convenience, the other Minitab file required for TMA 04, which already appeared in the module, is also available for download from the ‘Assessment’ area.*

Question 1, which covers topics in Unit 7, and Question 2, which covers topics in Unit 8, form M248 TMA 04. Question 1 is marked out of 23; Question 2 is marked out of 27.

Question 1 { 23 marks
You should be able to answer this question after working through Unit 7.
(a) Let X and Y be independent random variables both with the same
mean µ 6= 0. Define a new random variable W = aX + bY where a and
b are constants.
(i) Obtain an expression for E(W). [2]
(ii) What constraint is there on the values of a and b so that W is an
unbiased estimator of µ? Hence write all unbiased versions of W as
a formula involving a, X and Y only (and not b). [3]
(b) An otherwise fair six-sided die has been tampered with in an attempt to
cheat at a dice game. The effect is that the 1 and 6 faces have different
probability of occurring than the 2, 3, 4 and 5 faces.
Let θ be the probability of obtaining a 1 on this biased die. Then, the
outcomes of rolling the biased die have the following probability mass
function.
Table 1 The p.m.f. of outcomes of rolls of a biased die:

(i) By consideration of the p.m.f. in Table 1, explain why it is necessary for θ to be such that 0 < θ < 1=2. [2]
(ii) The value of θ is unknown. Data from which to estimate the value of θ were obtained by rolling the biased die 1000 times. The result of this experiment is shown in Table 2.

Table 2 Outcomes of 1000 independent rolls of a biased die

Show that the likelihood of θ based on these data is
L(θ) = C θ395 (1 − 2θ)605 where C is a positive constant, not dependent on θ. [5]
(iii) Show that L0(θ) = C θ394(1 − 2θ)604 (395 − 2000 θ): [4]

(iv) What is the value of the maximum likelihood estimate, θb, of θ based on these data? Justify your answer. What does the value of θb suggest about the value of θ for this biased die compared with the
value of θ associated with a fair, unbiased, die? [4]

c) Studies of the size and range of wild animal populations often involve tagging observed individual animals and recording how many times each is caught in a trap (from which it is then released back into the wild). The dataset presented in Table 3 consists of the numbers of times each of n = 334 wood mice were caught in a particular trap (over a two-year time period). The data are also provided in the Minitab file wood-mice.mtw.

Table 3 Numbers of trappings of wood mice

The geometric distribution with parameter p is a good model for these data.
(i) What is the maximum likelihood estimator of p for a geometric model? [1]
(ii) What is the maximum likelihood estimate of p for the data in Table 3? You are recommended to use Minitab to help you to answer this part of the question. [2]

Question 2 in Statistics
You should be able to answer this question after working through Unit 8.
(a) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)

Modern aircraft cockpit windscreens are complex items, comprising several layers of material and a heating system. Such windscreens are replaced upon damage to any of their components. A dataset was collected on the times to replacement of n = 84 windscreens of a particular modern airliner. The sample mean windscreen replacement time was 23 515 hours of flight. The sample standard deviation of windscreen replacement times was 5168 hours of flight.

(i) Obtain an approximate 90% confidence interval for the mean replacement time of this type of aircraft windscreen. What
property of the dataset justifies using this type of confidence interval, and why? [6]
(ii) Interpret the particular confidence interval that you found in part (a)(i) in terms of repeated experiments. [3]

(b) In this part of the question, you should calculate the required confidence interval by hand, using tables, and show your working. (You may use Minitab to check your answers, if you wish.)
In a large study of patients who were being treated for hypertension (high blood pressure), 148 out of 5493 patients receiving the conventional treatment for hypertension later suffered a stroke. Also,
192 out of 5492 patients receiving an alternative drug to treat their hypertension later suffered a stroke

(i) Obtain an approximate 95% confidence interval for the difference in proportions between the number of conventionally treated hypertension patients who later suffered a stroke and the number of hypertension patients treated with the alternative drug who later suffered a stroke. (You are advised to work with proportions rounded to four decimal places throughout; also, you may assume that the numbers involved are large enough that your approximation is a good one.) [5]

(ii) Some clinicians had suggested that the proportions of hypertension patients who suffered a stroke would not depend on which treatment they were being given. Are the data consistent with that
suggestion? Justify your answer briefly. [2]

(c) In various places in this module, data on the silver content of coins minted in the reign of the twelfth-century Byzantine king Manuel I Comnenus have been considered. The full dataset is in the Minitab file coins.mtw. The dataset includes, amongst others, the values of the silver content of nine coins from the first coinage (variable Coin1) and seven from the fourth coinage (variable Coin4) which was produced a number of years later. (For the purposes of this question, you can ignore the variables Coin2 and Coin3.) In particular, in Activity 8 and Exercise 2 of Computer Book B, it was argued that the silver contents in both the first and the fourth coinages can be assumed to be normally distributed. The question of interest is whether there were differences in the silver content of coins minted early and late in Manuel’s reign. You are about to investigate this question using a two-sample t-interval.

(i) Using Minitab, find either the sample standard deviations of the two variables Coin1 and Coin4, or their sample variances. Hence, check for equality of variances using the rule of thumb given in
Subsection 4.4 of Unit 8. [3]

(ii) Whatever the outcome of part (c)(i), use Minitab to obtain a 90% two-sample t-interval for the difference E(X1) − E(X4) where X1 denotes the mean silver content in coins of the first coinage and X4
denotes the mean silver content in coins of the fourth coinage.

State that interval and comment briefly on what it tells us about the silver content of coins in the earlier and later coinages. [3]

(iii) Name the distribution used in constructing the confidence interval in part (c)(ii), state the value of its parameter and show why the parameter takes the value that it does. [2]
(iv) What would have been the outcome if you had obtained a 90% two-sample t-interval for E(X4) − E(X1) instead of for

E(X1) − E(X4)? Justify your conclusion in terms of the derivative of the parameter transformation involved. [3]

If you need someone to help you with this statistics assignment, then MyMathLab homework help is the right platform to address all your statistics needs.

Minitab Data Analysis Project

This question is intended to assess your understanding of the use and interpretation of graphical and numerical summaries of data, and your use of MINITAB to obtain appropriate summaries.
You should be able to answer this question after working through Unit A1.
(a) The MINITAB worksheet alcohol.mtw contains data published in 1979 for fifteen countries on the average annual alcoholic consumption (in litres per person) and the death rate per 100000 of the population from cirrhosis and alcoholism. These data were discussed in Examples 1.5 and 3.2 of Unit A1. The worksheet contains three variables: country, consumption and deathrate.
(i) Produce a horizontal bar chart showing the alcohol consumption in each of the countries listed, with the following features:
• The countries should be ordered by alcohol consumption per person (highest at the top).
• The horizontal axis should be labelled ‘Alcohol consumption’
and the vertical axis labelled ‘Country’.
(ii) Produce a similar horizontal bar chart showing death rates from cirrhosis and alcoholism, with countries ordered by death rate [3]
(highest at the top). Label the horizontal axis appropriately.
(iii) Which countries have the same ranking in the two bar charts?
Which country has the lowest average consumption of alcohol?
Which country has the lowest death rate from cirrhosis and [3]
alcoholism.
(iv) Explain whether or not, in your view, comparing the bar charts in parts (a)(i) and (a)(ii) is a good way of investigating the relationship between alcohol consumption and death rate from cirrhosis and alcoholism. How might the bar charts be improved for [3]
this purpose?
(v) Suggest a better plot for investigating the relationship between [2]
alcohol consumption and death rate from cirrhosis and alcoholism. [1]
(b) The MINITAB worksheet bilirubin.mtw contains measurements of bilirubin (a reddish pigment of bile) made on 497 healthy individuals. The measurements are in mg/l (milligrams per litre), rounded up to the next whole number. The data are in the variable concentration.

(i)    Produce MINITAB’s default histogram for concentration. Briefly    

describe the main features of the distribution.
(ii) Now produce a histogram for concentration with midpoints at 0,1,... ,16 mg/l. Briefly explain why you might prefer this histogram to the default histogram that you obtained in [4]
part (b)(i).
(iii) Obtain and report the sample mean and the sample median of the variable concentration. Comment briefly on the relative size of the mean and the median, relating your comments to the shape of the histograms that you obtained in parts (b)(i) and (b)(ii). Obtain the sample skewness, and relate this to the shape of the [4]
histograms.

Question 2 – 25 marks
This question is intended to assess your understanding of the use and interpretation of graphical and numerical summaries of data, and your use of MINITAB to obtain appropriate summaries.
You should be able to answer this question after working through Unit A1.
The MINITAB worksheet pines.mtw contains data on the height (in cm) and age (in years) of 204 Japanese black pine trees (seedlings and saplings). The worksheet contains two variables: height and age.
(a) Obtain and report MINITAB’s default histogram for height. Why is the default histogram not a good representation of these data? Now produce a histogram that better represents the data. Describe a [6]
main feature of the data revealed by this histogram.
(b) Using MINITAB, obtain and report a scatterplot of height (on the vertical axis, labelled ‘Height (cm)’) against age (on the horizontal axis, labelled ‘Age (years)’).
Briefly describe the relationship between the two variables height and [5]
age.
(c) Calculate and report the standard deviation of height (correct to four decimal places) at each value of age. Arrange your results in a table showing the number of trees of each age and the standard deviation of the heights of the trees of each age. (The calculations can be done using either Display Descriptive statistics... or Store Descriptive statistics... . In the dialogue box, enter height in the Variables field and age in the By variables field.
Describe briefly how the standard deviation of the heights varies with [5]
age.
(d) Calculate and report the mean, median, standard deviation and [4]
interquartile range of the variable height. [4]
(e) Create a variable named height2 that excludes the values corresponding to the six outliers of height 150cm, but which otherwise includes the same values as the variable height, as follows.
• Obtain the Copy Columns to Columns dialogue box (Data > Copy > Columns to Columns...).
• In the Copy from columns field, enter height.
• Under Store Copied Data in Columns, select In current worksheet, in columns from the drop-down list, and enter height2 in its field.
• Uncheck Name the columns containing the copied data.
• Click on Subset the Data... to open the Copy Columns to Columns - Subset the Data dialogue box.
• Select Specify which rows to exclude (under Include or Exclude).
• Select Specify Which Rows To Exclude, select Rows that match and click on Condition....
• In the dialogue box that opens, enter height=150 in the Condition field, and click on OK.
• Click on OK, then click on OK again.
Calculate and report the mean, median, standard deviation and
interquartile range of the variable height2.
(f) Compare the numerical summaries that you obtained in part (e) with those that you obtained in part (d). Briefly discuss any differences that [4]
you observe in terms of resistant measures.
Question 3 – 27 marks
This question is intended to assess your understanding of the use and interpretation of graphical and numerical summaries of data, and your use of MINITAB to obtain appropriate summaries.
You should be able to answer this question after working through Unit A1 and Section 1 of Unit A2.
(a) The MINITAB worksheet gold.mtw contains 47 observations of gold assay, which is the recoverable gold content of gold ore (in grams per tonne). The worksheet contains one variable named assay.
(i) Use MINITAB to produce a horizontal boxplot of assay. Are the data left-skew, symmetric or right-skew? Describe two features of [3]
the boxplot that support your answer.
(ii) Based on the boxplot that you produced in part (a)(i), suggest appropriate measures of location and spread for the assay data. [5]
Explain your choice of measures, and calculate their values.
(iii) Create a variable named logassay that contains the natural logarithms of the gold assay values. Obtain and report a horizontal boxplot of logassay.
Describe the distribution of the transformed data, and comment briefly on the effect of the transformation on the appearance of the [3]
boxplot. [6]
(b) A nutritionist studying the effect of different proportions of protein in the diet of chicks randomly allocated some chicks to one of four groups, and recorded their weights (in grams) after three weeks’ growth. The four groups were normal diet, and low (10%), medium (20%) and high (40%) protein replacement diets. The data are stored in the MINITAB worksheet chicks.mtw. The worksheet contains four variables named normal, low, medium and high, corresponding to the four diet groups.
(i) Use MINITAB to produce a horizontal comparative boxplot of the two variables normal and high, with the common axis labelled ‘Weight (grams)’. Comment on the impact of the high protein

replacement diet on chick weight, as shown by this boxplot.    [7]

(ii) It might be expected that intermediate proportions of protein replacement would have less effect on weight than high proportions. Investigate whether or not this appears to be the case, as follows.
(1) Produce a second comparative boxplot in MINITAB that displays the values of all the four variables normal, low, medium and high.
(2) Based on the second comparative boxplot that you produced, briefly summarize the impact of diet on weight, accounting for

all four groups.    [6]

Question 4 – 22 marks
This question is intended to assess your understanding of the interpretation of tabular data, and your use of MINITAB to create a data file and produce appropriate summaries to explore and interpret data.
You should be able to answer this question after working through Unit A2 and Chapter 6 of Computer Book A.
The data in Table 1 were obtained from the website of the Office for National Statistics (ONS). For each of seven years, the table contains details of deaths in England and Wales for which Staphylococcus aureus (SA) or its antibody-resistant special form Methicillin-resistant Staphylococcus aureus (MRSA) was reported as a contributory factor on the death certificate. Note that patients who have MRSA when they die are usually patients who are already very ill, and their existing illness, rather than MRSA, is often designated as the underlying cause of death.
For each year listed, the table shows the number of death certificates that mentioned SA (some of which also mentioned a different underlying cause of death), the number of death certificates that described SA as the cause of death, and the number of death certificates that described MRSA as the cause of death. The death certificates in the second category (SA given as cause of death) form a subset of those in the first category (Mentioned SA), and the death certificates in the third category (MRSA given as cause of death) form a subset of those in the second category.
Table 1 Death certificates in England and Wales

    SA given as    MRSA given as

Year Mentioned SA cause of death cause of death
1994 448 148 14
1997 781 242 103
2000 1142 340 191
2003 1416 491 322
2006 2150 707 519
2009 1253 294 147
2012 557 117 38
(a) Without doing any calculations or drawing any graphs, comment on anytrends (that is, general tendencies to increase or decrease over the period for which the data are available) in the number of death certificates issued in England and Wales in each of the three categories. [3]
(b) (i) Enter the data in Table 1 in a MINITAB worksheet, giving the columns appropriate names. Check the accuracy of your data entry by calculating the total number of death certificates in each category: these should be 7747 (Mentioned SA), 2339 (SA given as cause of death) and 1334 (MRSA given as cause of death).
(ii) Create two variables, one named pSAcause containing the proportion of the death certificates that mentioned SA that gave SA as the cause of death, and one named pMRSAcause containing the proportion of the death certificates for which SA was given as the cause of death that actually specified MRSA as the cause of death. Display the proportions rounded to three decimal places.
(You can do this using Calculator... from the Calc menu.)
(iii) Include a printout of your MINITAB worksheet with your TMA. [7]
(c) (i) Use MINITAB to produce a multiple line plot showing the variation over time in the number of death certificates in each of the three categories. (Hint: The simplest way of doing this is using
Scatterplot... from the Graph menu and selecting With Connect Line in the Scatterplots dialogue box. In the Scatterplot: With Connect Line dialogue box, enter the variable for ‘Mentioned SA’ under Y variables and Year under X variables in row 1, enter the variable for ‘SA given as cause of death’ under Y variables and Year under X variables in row 2, and enter the variable for ‘MRSA given as cause of death’ under Y variables and Year under X variables in row 3. Click on
Multiple graphs... to obtain the Scatterplot: Multiple Graphs dialogue box. Make sure that Overlaid on the same graph is selected under Show Pairs of Graph Variables.) Edit the horizontal scale so that ticks are included only at the years listed in Table 1. Make sure that the vertical axis is appropriately

labelled.    [4]

(ii) Comment briefly on the trends that are clear from the plot. [2]
(d) (i) Use MINITAB to produce a multiple line plot showing the variation over time in the proportion of the death certificates that mentioned SA for which SA was given as the cause of death
(pSAcause) and the proportion of the death certificates that gave SA as the cause of death that actually specified MRSA as the cause of death (pMRSAcause). Make sure that the vertical axis is

appropriately labelled.    [2]

(ii) Comment briefly on any trends in these proportions that are

evident from the plot.    [4]

 
TMA 02 Cut-off date 12 January 2017
You are advised to look again at the section entitled General advice on TMAs at the beginning of this Assignment Booklet.
Questions 1 to 5 below, on Units A3, A4 and A5, form tutor-marked assignment M248 02. Question 1 (on Unit A3) is marked out of 17. Question 2 (on Units A3 and A4) is marked out of 22. Question 3 (on Unit A4) is marked out of 25. Questions 4 and 5 are on Unit A5; Question 4 is marked out of 14, and Question 5 is marked out of 22.
Question 1 – 17 marks
This question is intended to assess your understanding of probability functions and of the probability models introduced in Unit A3.
You should be able to answer this question after working through Unit A3.
(a) (i) Give one reason why the following function cannot be a probability mass function:

 .    [2]

(ii) Give one reason why the following function cannot be a probability density function:

 .    [2]

(iii) Give one reason why the following function cannot be thecumulative distribution function of a continuous random variable X that only takes values between 0 and 3:

 .    [2]

(b) Records show that 8% of blood samples tested for a certain condition test positive. Assuming that whether or not a blood sample tests positive is independent of whether or not any other blood sample tests positive, calculate by hand the following probabilities to three significant figures. In each case, state clearly the probability model that you use (including the values of any parameters).

(i)    The probability that, out of 20 samples tested, at least four will    

test positive.

(ii)    The probability that the first blood sample that tests positive    [7]

tomorrow will be the tenth sample tested. [4]

Question 2 22 marks
This question is intended to assess your understanding of the binomial distribution as a model for data.
You should be able to answer this question after working through Units A3 and A4.
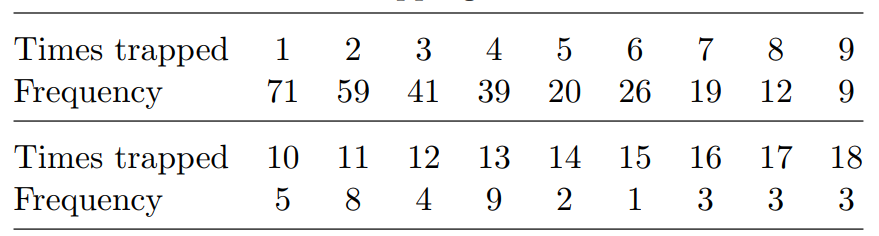
The MINITAB worksheet absences.mtw contains the numbers of absences of 113 students from a course of 24 lectures.
(a) Calculate and report the mean and standard deviation of the number of absences of students from the course. An estimate of p, the proportion of lectures missed per student, is given by the mean number of lectures missed divided by 24. Estimate p, giving your answer rounded to four
decimal places.
(b) Using MINITAB, produce a bar chart of the number of absences of the students, with a suitable title, the horizontal axis labelled ‘Number of absences’ and the vertical axis labelled ‘Frequency’.
It is suggested that an appropriate model for the number of lectures missed by a student might be a binomial distribution B(24,p). What assumptions are made by using this model? In your opinion, is a [3]
binomial model appropriate? Briefly justify your answer.
(c) Obtain a frequency distribution of the number of lectures missed by the students. (Try using Tally Individual Variables... from the Tables submenu of Stat.) You should include the frequency distribution, which need not be as MINITAB output, with your answer.
Calculate and report the proportions of students who missed
0,1,2,... ,12 lectures. Give the proportions rounded to four decimal [6]
places.
(d) Calculate and report the probability that a student will miss
0,1,... ,11, ≥12 lectures, assuming that the number of lectures missed by a student has the binomial distribution B(24,p), where p is the estimate that you obtained in part (a). Give the probabilities rounded [4]
to four decimal places. (You may use MINITAB for this, if you wish.)
(e) Comment briefly on how close the observed proportions of students who missed 0,1,... ,11, ≥12 lectures are to those predicted by the binomial model. What does this suggest about the appropriateness, or otherwise, [4]
of the binomial model?
(f) Calculate and report the standard deviation of the binomial distribution B(24,p), where the value of p is the estimate that you found in part (a). Given the sample standard deviation of the number of absences that you obtained in part (a), what do you conclude from this about the [2]
appropriateness, or otherwise, of the binomial model? [3]
Question 3 25 marks
This question is intended to assess your understanding of probability mass functions and cumulative distribution functions for discrete random variables, and of one of the probability models introduced in Unit A4.
You should be able to answer this question after working through Unit A4.
(a) The probability mass function of a discrete random variable X is given in Table 2.

Table 2    The p.m.f. of X

x    0    1    2    3    4    5    6
p(x)    0.05    0.05    0.10    0.25    0.3    0.15    0.10

(i)    Calculate and report P(X > 3) and P(1 < X < 4).    [3]
(ii)    Calculate and report the mean of the random variable X.    [2]

(iii) Calculate and report the variance of the random variable X.
(iv) Write down a table containing values of F(x), the cumulative [3]
distribution function of X, for x = 0,1,2,3,4,5,6.

(v)    Write the probabilities P(X > 3) and P(1 ≤ X ≤ 4) in terms of the

c.d.f. F(x). Use the c.d.f. to calculate and report the values of [2]
these two probabilities.
(b) The MINITAB worksheet geese.mtw contains information on the sizes of 45 flocks of snow geese, estimated using different methods. This question concerns the variable photo, which contains the flock counts based on photographic evidence. It is suggested that a geometric distribution might be suitable for modelling the variation in flock size.
(i) Use MINITAB to produce a histogram of the data in the variable photo, with the first interval starting at 0, and using an appropriate interval width.
Calculate and report the mean and standard deviation of the flock [5]
sizes (to one decimal place).
(ii) An estimate of p, the parameter of the geometric distribution, is given by p = 1/x, where x is the sample mean that you calculated in part (b)(i). Calculate and report this estimate of p, giving your estimate rounded to four decimal places, and obtain the standard deviation of the geometric distribution that has this rounded value for the parameter p. Compare this standard deviation with the [3]
sample standard deviation that you found in part (b)(i).
(iii) Give one reason to support using the geometric model for these data, and one reason against using the model. What do you conclude about the appropriateness, or otherwise, of using this [4]
model for these data? [3]
Question 4 14 marks
This question is intended to assess your understanding of the properties of data from a Poisson process, and of graphical methods for assessing whether a Poisson process is an appropriate model for data.
You should be able to answer this question after working through Unit A5.
The lengths of time (in minutes, recorded to the nearest minute) between successive goals being scored in the football matches in the 1990, 1994, 1998 and 2002 World Cup tournaments are in the variable intergoaltime in the worksheet worldcup.mtw. (Each time is the number of minutes of football played between successive goals.)
(a) Without drawing any graphs, check whether these data are consistent with an exponential distribution being a good model for the intervals
between goals being scored.
(b) Suggest a suitable graph to investigate whether or not an exponential distribution might be a good model for the intervals between goals [3]
being scored. Using MINITAB, produce the graph.
(c) On the basis of the graph that you produced in part (b), do you think that an exponential distribution is a plausible model for these data? [3]
Explain your answer.
(d) The data are listed in the order in which they arose.
(i) Using MINITAB, produce an appropriate graph to investigate whether, for the period of observation, the data are consistent with the rate at which goals were scored remaining constant over the [2]
course of the four tournaments.
(ii) On the basis of your graph, explain whether or not you think that the rate at which goals were scored remained constant over the course of the four tournaments. If you think that the rate did not [3]
remain constant, then say how you think it changed. [3]
Question 5 22 marks
This question is intended to assess your understanding of the Poisson process.
You should be able to answer this question after working through Unit A5.
In this question, you should calculate all the probabilities without using MINITAB, and show your working. (You may, of course, use MINITAB to check your answers, if you wish.)
Suppose that the arrivals of emergency calls at an ambulance station during daylight hours may be modelled as a Poisson process with rate 7.5 per hour.
(a) (i) Write down the distribution of the number of emergency calls in a one-hour period, including the values of any parameters. [2]
(ii) Calculate and report the probability that exactly five emergency

calls arrive in an hour.    [2]

(iii) Calculate and report the probability that more than three

emergency calls arrive in an hour.    [4]

(b) (i) Write down the distribution of the number of emergency calls arriving in a twenty-minute period, including the values of any

parameters.    [2]

(ii) Calculate and report the probability that at most two emergency

calls arrive in twenty minutes.    [3]

(c) (i) Write down the distribution of the waiting time (in hours) between the arrival of two successive emergency calls, including the values of

any parameters.    [2]

(ii) Calculate and report the probability that the gap between the arrival of two successive emergency calls will be more than five

minutes, but less than ten minutes.    [5]

(iii) Calculate and report the probability that the gap between thearrival of two successive emergency calls will be less than three

minutes.    [2]

TMA 03 Cut-off date 30 March 2017
You are advised to look again at the section entitled General advice on TMAs at the beginning of this Assignment Booklet.
In this assignment, you are advised to use MINITAB to do the statistical calculations wherever possible.
Questions 1 to 5 below, on Unit B3 and Block C, form tutor-marked assignment M248 03. Question 1 (on Unit B3) is marked out of 10. Questions 2 and 3 are on Unit C1; Question 2 is marked out of 16, and Question 3 is marked out of 16. Question 4 (on Unit C2) is marked out of 31. Question 5 (on Unit C3) is marked out of 27.
Question 1 – 10 marks
This question is intended to assess your understanding of confidence intervals and their interpretation.
You should be able to answer this question after working through Unit B3.
In a study of inattention while driving, 453 drivers who had been deemed to have been responsible for a crash were questioned by researchers. The researchers determined that for 243 of these drivers, their mind was wandering immediately prior to the crash. Based on these data, an approximate 99% confidence interval, calculated using large-sample methods, for the proportion of drivers responsible for a crash whose mind was wandering just before the crash is (0.475,0.597).
In parts (a) and (b), you should adapt the repeated experiments and plausible ranges interpretations of a confidence interval given in Section 2 of Unit B3 (and in the Handbook) to this particular context and confidence interval.
(a) Interpret the confidence interval using the repeated experiments interpretation by filling in the gaps in the template below.
If a large number of samples of ...... were drawn independently from
............, and on each occasion ............, then ............ would contain
............ .
(b) Interpret the confidence interval using the plausible ranges interpretation by filling in the gaps in the template below.
The confidence interval (0.475,0.597) defines a plausible range for ...., ...... in the following sense.
If ...... were greater than ......, then the probability of observing ......... less than or equal to ...... would be less than ...... . Similarly, if ...... were less than ......, then the probability of observing ......... would be less [3]
than ...... .
(c) It has been suggested that an adult’s mind wanders 50% of the time when they are awake. Are the data consistent with 50% of drivers’ minds wandering at the time of a crash for which they are responsible? [5]
Justify your answer briefly. [2]
Question 2 – 16 marks
This question is intended to assess your understanding of significance testing.
You should be able to answer this question after working through Sections 1 to 4 of Unit C1.
In a study of aids to smoking cessation, researchers randomized some smokers who were keen to quit to use either nicotine e-cigarettes or nicotine patches. After six months, the researchers recorded whether the smokers were still not smoking. Of the 289 smokers who used the nicotine e-cigarettes, 21 were still not smoking after 6 months. Of the 295 smokers who used the nicotine patches, 17 were still not smoking after 6 months.
(a) (i) Among smokers using nicotine e-cigarettes to help them quit, what distribution provides a model for the number of smokers who were
still not smoking 6 months later? Explain the meaning of any

symbols that you use.    [2]

(ii) Among smokers using nicotine patches to help them quit, what distribution provides a model for the number of smokers who were still not smoking 6 months later? Explain the meaning of any

symbols that you use.    [2]

(iii) Using the notation that you used in parts (a)(i) and (a)(ii), writedown the null and alternative hypotheses to be used to test whether the proportion of smokers using nicotine e-cigarettes to help them quit who were still not smoking after 6 months is
different to the proportion of smokers using nicotine patches to

help them quit who were still not smoking after 6 months.    [1]

(b) In this part of the question, you are asked to carry out a significancetest for the null and alternative hypotheses that you suggested in part (a)(iii).
(i) State the formula of your choice of test statistic D, and calculate

by hand the observed value of D for this test.    [2]

(ii) State the appropriate null distribution of the test statistic D,

calculating parameters by hand where appropriate.    [3]

(iii) Using MINITAB, obtain and report, correct to three decimalplaces, the significance probability for the test. Explain how the value of the test statistic reported by MINITAB can be calculated from the observed value of D that you calculated in part (b)(i). [3]
(iv) State your conclusions from the test. [3]
(v) Question 3 – 16 marks
This question is intended to assess your understanding of fixed-level testing and power.
You should be able to answer this question after working through Unit C1.
(a) The MINITAB worksheet tobacco.mtw contains data on the number of lesions found on tobacco leaves contaminated with viruses. Each tobacco leaf was contaminated by two virus preparations, labelled A and B. One half of the leaf was exposed just to A, and the other to B. For each of eight leaves, variable Alesions gives the number of lesions found on the half exposed to virus preparation A, and variable Blesions gives the number found on the half exposed to virus preparation B.
Create a variable diff = Alesions - Blesions containing the differences between the numbers of lesions. Assume that the differences can be modelled using a normal distribution whose mean and standard deviation are not known.
(i) In this part of the question, you are asked to carry out a fixed-level test, using a 5% significance level, of the null hypothesis H0 : µ = 0, where µ is the population mean difference between the number of lesions on the half exposed to virus preparation A and the number on the half exposed to virus preparation B.
• Write down the alternative hypothesis.
• State the test statistic, and write down the null distribution of this test statistic.
• Obtain the rejection region of the test statistic.
• Write down the observed value of the test statistic. (You
should use MINITAB to obtain this.) [7]

(ii)    State your conclusions from the test.

(b) A second study is now proposed to try to replicate the results. The two virus preparations A and B will again be used to contaminate halves of tobacco leaves. The intention in this second study is to use a fixed-level test with a 1% significance level. It is also decided that the power of the test to distinguish a true underlying mean difference of 1.5 should be 90%. In order to calculate the sample size required, the researchers are prepared to assume that the population standard deviation of the differences in the numbers of lesions will be close to the sample standard deviation in the study in part (a).
Use MINITAB to calculate the size of the sample that is required. Write down the input values that you supplied to MINITAB to perform this [5]
calculation, as well as the required sample size. [4]
Question 4 – 31 marks
This question is intended to assess your understanding of nonparametric tests.
You should be able to answer this question after working through Unit C2.
(a) The ages at death of male members of four Scottish clans were collected. The clans are simply identified as Clan A, Clan B, Clan C and Clan D. The variable Aclan in the MINITAB worksheet clans.mtw contains the ages at death for men in Clan A. Similarly, the variables Bclan, Cclan and Dclan contain the ages at death for samples of men in Clans B, C and D, respectively.

(i) One question of interest is whether men in these clans on average ‘lived three score years and ten’, that is, lived until they were 70. Create a column in your MINITAB worksheet that contains all the ages at death. By producing an adequate plot, explain why it would not be appropriate to make an assumption of normality for
the age at death for clansmen from one of these clans.
(ii) Carry out a two-sided test of the null hypothesis that the underlying median age at death for men from these clans is 70.
Explain briefly the advantage of using the Wilcoxon signed rank test rather than the sign test. Also briefly explain whether there are any disadvantages of using the Wilcoxon signed rank test rather than the sign test with these data.
Carry out both a sign test and a Wilcoxon signed rank test of the [3]
null hypothesis. What do you conclude?
(iii) The test that you carried out in the previous part implicitly assumed that the distribution of the age at death for clansmen is the same for each of the four clans. In order to begin to investigate the reasonableness of this assumption, Clan A will be compared with Clan B.
Use an appropriate test (justifying your choice) to investigate whether there is a difference in location between the age at death for men in Clan A and age at death for men in Clan B. Report [7]
your conclusions.
(b) The variable temperature in the Minitab worksheet climate.mtw is given to two decimal places. But to what extent does this reflect the actual accuracy to which the data are recorded? One way to investigate this is to consider the distribution of the digits in the second decimal place. Given that the temperatures range from 7.80◦C to 11.53◦C, it could be assumed that the digits in the second decimal place have a uniform distribution. That is, every digit is equally likely to appear. So is this assumption reasonable for the variable temperature? This is what you are going to investigate in this part of the question.
(i) In Table 3, the number of times each digit from 0 to 9 occurred in the second decimal place for the variable temperature is given. Table 3 Occurrence of digits in the second decimal place [8]

Digit 0 1 2 3 4 5 6 7 8 9
Observed frequency 34 1 0 34 0 0 0 31 0 0

Obtain the expected frequencies of the digits 0,1,2,3,4,5,6,7,8,9 assuming a uniform distribution.
Without doing any further calculations, comment on the quality of
fit of the uniform model.
(ii) In the next part you will carry out a chi-squared test of goodness of fit of the uniform distribution to these data. Why is it not [4]
necessary to pool categories first?
(iii) Carry out a chi-squared test of goodness of fit of the uniform [1]
distribution to these data. Report your conclusions carefully. [8]
Question 5 – 27 marks
This question is intended to assess your understanding of the modelling process.
You should be able to answer this question after working through Unit C3.
(a) In a road safety study, the lengths of time (in milliseconds) thatpedestrians had to wait at a particular point before crossing the road were recorded.
(i) Discuss briefly whether the times that the pedestrians waited
should be regarded as continuous or discrete.
(ii) Based only on the context in which the data were obtained, suggest a model for the length of time that pedestrians waited, giving [2]
reasons for your choice. [3]
(b) In a study, the numbers of T4 and T8 cells in the blood of patients inremission from one of two diseases, Hodgkin’s disease and non-Hodgkin’s disseminated malignancies, were measured. Each measurement corresponds to the number of cells per cubic millimetre of blood.
A statistician analysed the data for the T4 cells. During his analysis, he made the following notes:
Used MINITAB version 17. MINITAB worksheet hodgkins.
Data source: Shapiro, C.M., Beckmann, E., Christiansen, N., Bitran, J.D., Kozloff, M., Billings, A.A. and Telfer, M.C. (1987) Immunologic status of patients in remission from Hodgkin’s disease and disseminated malignancies. American J. Medical Sciences, 293, 366–70.
Data: lT4hodgkins = ln(T4hodgkins) and lT4nonhodgkins = ln(T4nonhodgkins).
Hodgkin’s disease: 20 patients, mean 6.487, standard deviation 0.708, range 5.142 to 7.789.
Non-Hodgkin’s disease: 20 patients, mean 6.089, standard deviation 0.632, range 4.754 to 7.132.
Checked normality using probability plots: OK.
Ratio of variances: 0.502/0.399 ≃ 1.26.
Mean difference 0.398, with 95% CI (−0.031,0.828).
Two-sample t-test: t = 1.88, df = 38, p = 0.068.
More T4 cells in the blood of Hodgkin’s disease patients.
Using these notes as a guide, write a brief statistical report of this statistician’s analysis. Your report should include the following sections:
• Summary (4 marks)
• Introduction (3 marks)
• Methods (6 marks)
• Results (6 marks)
• Discussion (3 marks)
Your completed report should be similar in style and length to the completed statistical report in Subsection 4.2 of Unit C3. [22]

TMA 04 Cut-off date 11 May 2017
You are advised to look again at the section entitled General advice on TMAs at the beginning of this Assignment Booklet.
In this assignment, you are advised to use MINITAB to do the statistical calculations wherever possible.
Note that the MINITAB data files required for this assignment are not part of the M248 data files and must be downloaded from the ‘TMA resources’ area of the ‘Assessment resources’ block on the M248 website.
Questions 1 to 4 below, on Units D1, D2 and D3, form tutor-marked assignment M248 04. Question 1 (on Unit D1) is marked out of 36.
Question 2 (on Unit D2) is marked out of 25. Questions 3 and 4 are on Unit D3; Question 3 is marked out of 25, and Question 4 is marked out of 14.
Question 1 – 36 marks
This question is intended to assess your understanding of point estimation.
You should be able to answer this question after working through Unit D1.
(a) The data in Table 4 relate to the classification of 134 recorded crimes(occurring during a month in a certain UK postcode area) into five crime categories.

Table 4    Classification of crimes

Crime categories    1    2    3    4    5
Observed frequency    25    14    42    11    42

A possible model for these data is the one indexed by a parameter θ, where 0 < θ < 1, with the following probabilities of categories 1,2,3,4,5, respectively:
.
(i) Show that the likelihood of θ for these data has the form
,
where c is a number and does not involve θ. (You should show how
c is formed, but you do not need to evaluate its value.)
(ii) Ignoring c, the log-likelihood is [4]
.
Use MINITAB to evaluate l(θ) at θ = 0.05,0.10,0.15,... ,0.95.
Give the values of l(θ) in a table, and produce a graph in which
l(θ) is plotted against θ for each of these values.
(iii) Correct to two decimal places, the value of θ that maximizes l(θ) is 0.90. Find θb, the maximum likelihood estimate of θ, correct to three decimal places. Include sufficient detail in your answer to [6]
show how you obtained this value. [5]

(iv) Calculate and report the estimated probabilities of the five categories when the value of θ is equal to θb, the maximum likelihood estimate of θ that you obtained in part (a)(iii).
Hence determine the expected number of the 134 crimes in each of the five categories based on this model. Make sure that you retain sufficient decimal places throughout your calculations to ensure reasonable accuracy for the expected frequencies. Without performing a test, comment on the fit of this model to the observed data.
If you wanted to test the fit of the model to the data, what test
would you use?
(b) The MINITAB worksheet bosch.mtw (from the M248 website) contains data about a Bosch car battery. The column price gives the price (to the nearest £) from each of 23 vendors. Suppose that these observations are a random sample from a normal distribution N(µ,σ2).

(i)    Use MINITAB to obtain unbiased estimates of the population    [6]

mean µ and the population variance σ2.

(ii)    Use your answers to part (b)(i) to obtain maximum likelihood    [2]

estimates of µ and σ2.
(iii) Use a fixed-level test with a 5% significance level to test the null hypothesis that the variance σ2 takes the value 400 in £2 against the alternative hypothesis that σ2 differs from this value. State [3]
your conclusions carefully.
Question 2 – 25 marks
This question is intended to assess your understanding of linear regression.
You should be able to answer this question after working through Unit D2.
An investigation to determine a possible relationship between the number of red blood cells (RBC) and the so-called packed cell volume (PCV) in blood (that measures the percentage of the blood occupied by red blood cells) used blood samples taken from 10 dogs. The data are recorded in the MINITAB worksheet bloodcells.mtw (from the M248 website). The variable PCV (in %) is stored in the column volume, and the variable RBC (counts in millions) is given in the column count. This question is concerned with how the RBC counts depend on the PCV of blood.
(a) (i) Obtain a scatterplot of count on the vertical axis against volume. [10]
Briefly describe the relationship between the variables.
(ii) Fit a linear regression model to the data in the columns volume and count. State the fitted model.
Check the assumptions of the linear regression model. You should include any plots that you produce with your answer, and explain whether you think that the assumptions are reasonable for these data.
State, giving a brief reason, whether you think a linear regression [5]
model might be appropriate for these data. [11]
(b) Assume that the linear regression model fitted in part (a) is appropriate.
(i) Carry out a test to check whether count depends on volume. [4]
(ii) Calculate a 99% confidence interval, with values rounded to one

decimal place, for the RBC counts for a PCV of 53%.    [2]

(iii) Calculate the prediction and a 90% prediction interval, with valuesrounded to one decimal place, for the RBC counts for a PCV

of 43%.    [3]

Question 3 – 25 marks
This question is intended to assess your understanding of correlation.
You should be able to answer this question after working through Unit D3.
The MINITAB worksheet carbohydrate.mtw (from the M248 website) contains the percentages of total calories obtained from complex carbohydrates, for 20 male insulin-dependent diabetics who had been on a high-carbohydrate diet for six months. The records for the 20 diabetics are given in the columns carbohydrate and weight.
(a) (i) Obtain a scatterplot of carbohydrate against weight. Briefly

describe the relationship between the two variables.    [5]

(ii) Which correlation coefficient would you use to measure the correlation between carbohydrate and weight? Explain your

answer.    [2]

(b) (i) Irrespective of your answer in part (a)(ii), calculate the Pearson correlation coefficient between carbohydrate and weight. How strong is the Pearson correlation between these variables? [3]
(ii) Use the Pearson correlation to test for no association between

carbohydrate and weight. State your conclusion.    [4]

(c) (i) Irrespective of your answer in part (a)(ii), calculate the Spearman rank correlation coefficient between carbohydrate and weight. How strong is the Spearman rank correlation between these

variables?    [3]

(ii) Use the Spearman rank correlation to test for no association between carbohydrate and weight. State your conclusion. Why
might it not be appropriate to use the approximate test for no

association with these data?    [5]

(d) Compare the correlation coefficients that you found in parts (b)(i)
and (c)(i). What do you conclude? [3]

Question 4 – 14 marks
This question is intended to assess your understanding of conditional probability and of association in contingency tables.
You should be able to answer this question after working through Unit D3.
A study was carried out by a health authority to investigate the relationship between the regular use of aspirin and gastric ulcers in patients of a hospital. A sample of patients with and without a gastric ulcer (who were similar with respect to age, gender and socio-economic status) completed a questionnaire. On the basis of their answers, each patient was classified as either with or without a gastric ulcer, and as either being or not being a regular user of aspirin. Table 5 reports the resulting data.
Table 5 Gastric ulcers and aspirin use

Regular user of aspirin?
Gastric ulcer No Yes
With 39 25
Without 62 6
(a) Use the data in Table 5 to estimate the following probabilities, giving your answers correct to two decimal places.

(i)    The probability that a patient has a gastric ulcer, given that he or    

she is a regular user of aspirin.

(ii)    The probability that a patient is not a regular user of aspirin, given    [2]

that he or she has a gastric ulcer.
(b) Enter the data in Table 5 into a MINITAB worksheet (include a printout of the worksheet in your report), and carry out a test for no association between the regular use of aspirin and gastric ulcers, for [2]
patients of the hospital. Report your conclusion. [10]

Would you like to get help with this project? At, MyMathlab Homework help.com, we are always available to help you with any statistics project. We have solved this project before, and we can provide you with the solutions if you so wish.

Data Analysis Using Minitab
(Using Minitab Answer the following) Consider a manufacturing plant that produces high-quality products primarily using skilled labor. They are concerned about defects found in the surface coating for their product and have been exploring potential improvement strategies. Note that each prompt below may require more than one visualization and/or analysis to fully answer.

1. Previous study showed that there is a difference in Quality ratings based on the Team. Considering this, they would like to test four potential factors (Line, Method, Temperature, and Humidity) while controlling for the effect of Team. Using the provided data, create a 2k factorial model by restructuring the Method factor as two, two-level factors and treating Team as a four-level blocked variable. Use Minitab to generate a 25-2 model blocked by replicates and extract the relevant data from the provided dataset to complete the analysis. Discuss the validity, fit, and reliability of the model and interpret the results including addressing any important aliased relationships.
2. Identify the treatment combinations that would be needed to complete the full fold-over for this design and briefly discuss how the fold-over model would help to interpret the results from Part 2. Complete the full fold-over, discuss the validity, fit, and reliability of the model, and interpret the results.
3. Use a general full factorial DOE model to evaluate the original five factors using their defined levels (a mixed-level design). Discuss the validity, fit and reliability of the model and interpret the results.